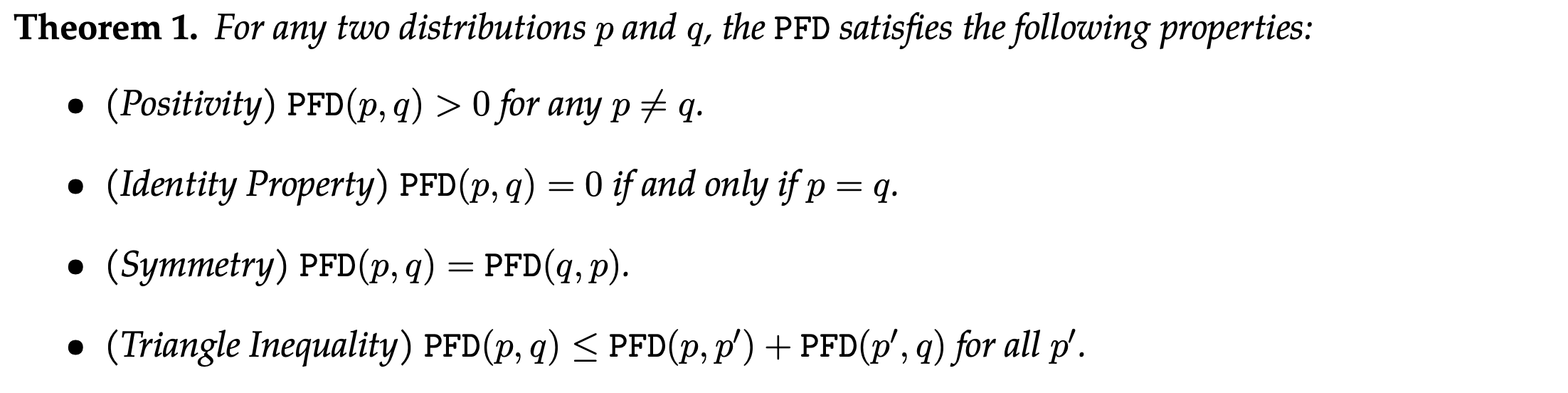Understanding Generalization in Diffusion Models via Probability Flow Distance

Huijie Zhang1, Zijian Huang2, Siyi Chen1, Jinfan Zhou1, Zekai Zhang1, Peng Wang1, Qing Qu1
1Department of Electrical and Computer Engineering, University of Michigan
2Department of Industrial and Operations Engineering, University of Michigan
Paper arXiv

Abstract

Diffusion models have emerged as a powerful class of generative models, capable of producing high-quality samples that generalize beyond the training data. However, evaluating this generalization remains challenging: theoretical metrics are often impractical for high-dimensional data, while no practical metrics rigorously measure generalization. In this work, we bridge this gap by introducing probability flow distance (PFD), a theoretically grounded and computationally efficient metric to measure distributional generalization. Specifically, PFD quantifies the distance between distributions by comparing their noise-to-data mappings induced by the probability flow ODE. Moreover, by using PFD under a teacher-student evaluation protocol, we empirically uncover several key generalization behaviors in diffusion models, including:

  • Scaling behavior from memorization to generalization.
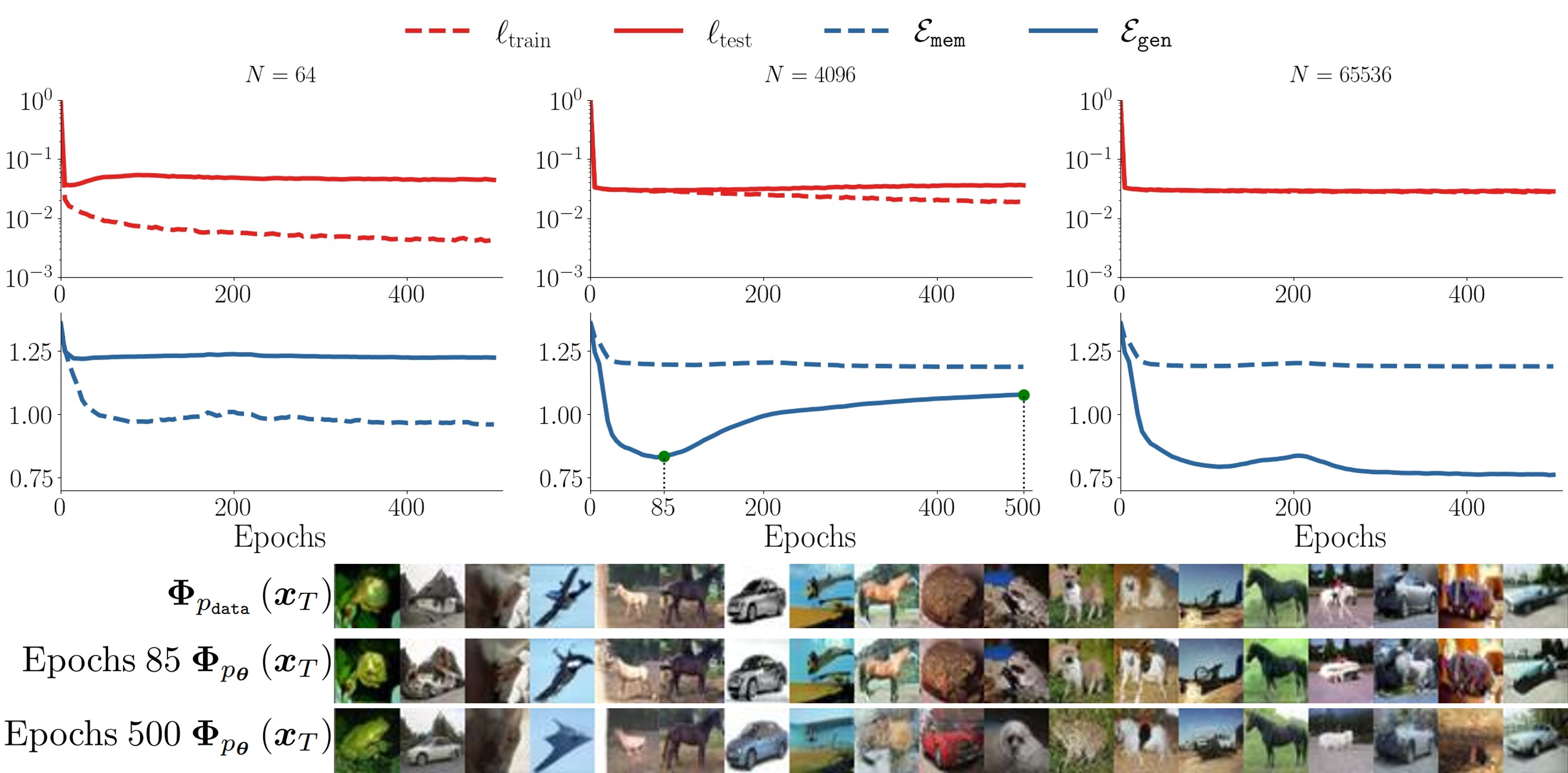
  • Early learning and double descent training dynamics.
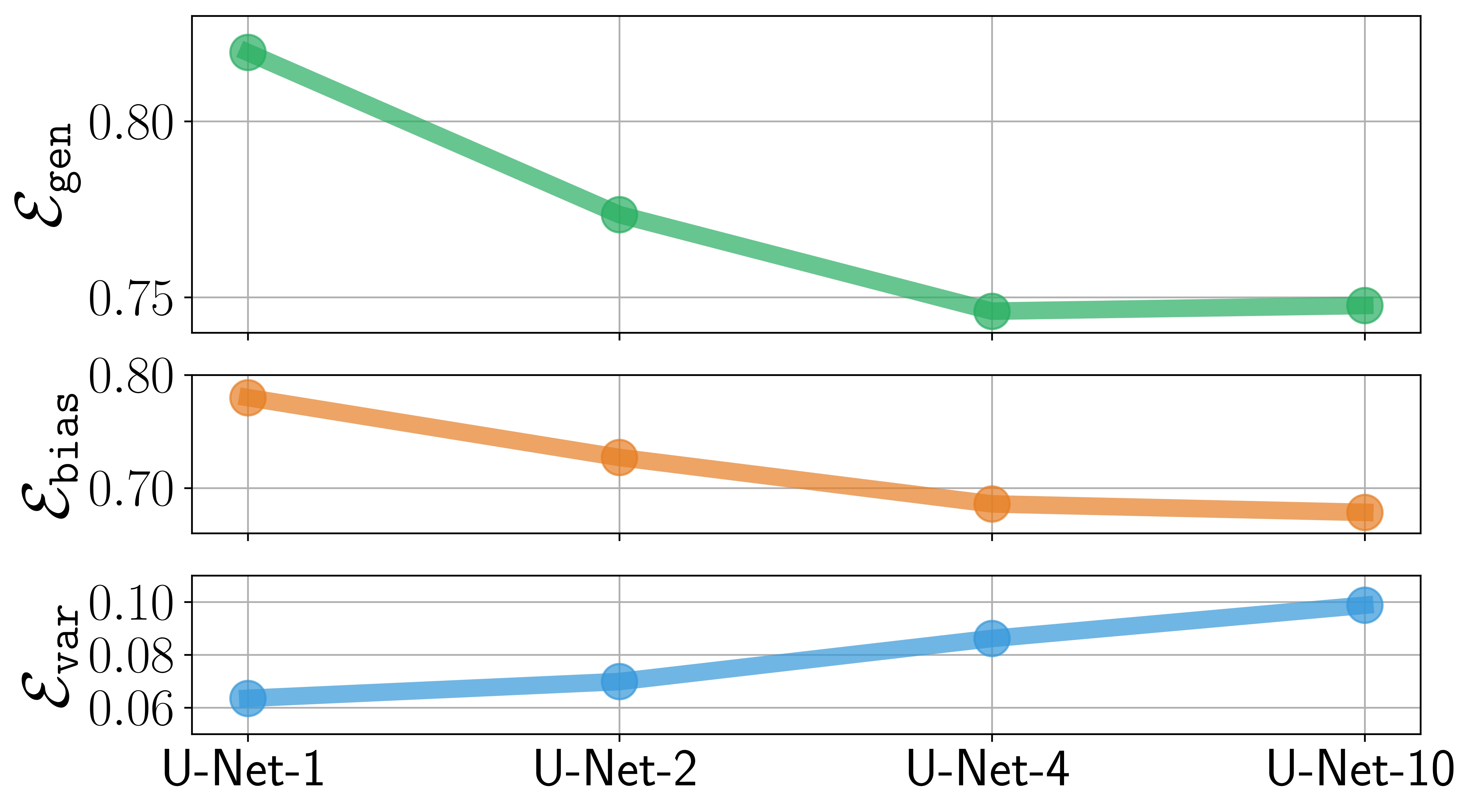
  • Bias-variance decomposition.
Beyond these insights, our work lays a foundation for future empirical and theoretical studies on generalization in diffusion models.

Measuring Distribution Distance via Probability Flow Distance

We define a metric to measure the distance between any two distributions as follows:

Under Definition 1, we show that PFD satisfies the axioms of a metric:

And PFD is guaranteed to be approximated to arbitrary precision by its empirical estimate with high probability, givem a finite number of samples:

Quantifying Generalization Error of Diffusion Models

Based on PFD, we formally define memorization and generation as follows:

To have access to underlying data distributions, we propose a teacher-student evaluation protocol to measure the generalization error of diffusion models. More details can be found in our paper.

Measuring Key Generalization Behaviors in Diffusion Models

Based on the evaluation protocol, this section reveals several key generalization behaviors in diffusion models: (i) MtoG scaling behaviors with model capacity and training size, (ii) early learning and double descent in learning dynamics, and (iii) bias-variance trade-off of generalization error.

Scaling Behaviors of the MtoG Transition

Scaling behavior in the MtoG transition. \(\mathcal{E}_{\mathtt{mem}}\) and \(\mathcal{E}_{\mathtt{gen}}\) plotted against \(\log_2(N)\) for a range of U-Net architectures (U-Net-1 to U-Net-10). Right: the same metrics plotted against \(\log_2\left(\frac{N}{\sqrt{|\boldsymbol \theta|}}\right)\), where \(|\boldsymbol \theta|\) is the number of model parameters.

Early Learning and Double Descent in Learning Dynamics

Training dynamics of diffusion models in different regimes. The top figure plots \(\mathcal{E}_{\mathtt{mem}}\), \(\mathcal{E}_{\mathtt{gen}}\), \(\ell_{\texttt{train}}\), \(\ell_{\texttt{test}}\) over training epochs for different dataset sizes: \(N = 2^6\) (left), \(2^{12}\) (middle), \(2^{16}\) (right). The bottom figure visualizes the generation when \(N = 2^{12}\). The top row shows samples from the underlying distribution \(\boldsymbol \Phi_{p_{\texttt{data}}}(\boldsymbol{x}_T)\), while the middle and bottom rows display outputs from the trained diffusion model \(\boldsymbol \Phi_{p_{\boldsymbol \theta}}(\boldsymbol{x}_T)\) at epoch 85 and 500, respectively.

Bias-variance Trade-off of the Generalization

Bias-Variance Trade-off. (a) plots the generalization error \(\mathcal{E}_{\mathtt{gen}}\), bias \(\mathcal{E}_{\mathtt{bias}}\), and variance \(\mathcal{E}_{\mathtt{var}}\) across different network architectures with a fixed training sample size of \(N = 2^{16}\). (b) shows \(\mathcal{E}_{\mathtt{bias}}\) and \(\mathcal{E}_{\mathtt{var}}\) as functions of the number of training samples \(N\) for various network architectures.

BibTeX

@article{zhang2025understanding,
        title={Understanding Generalization in Diffusion Models via Probability Flow Distance},
        author={Zhang, Huijie and Huang, Zijian and Chen, Siyi and Zhou, Jinfan and Zhang, Zekai and Wang, Peng and Qu, Qing},
        journal={arXiv preprint arXiv:2505.20123},
        year={2025}
      }