(a)
(b)
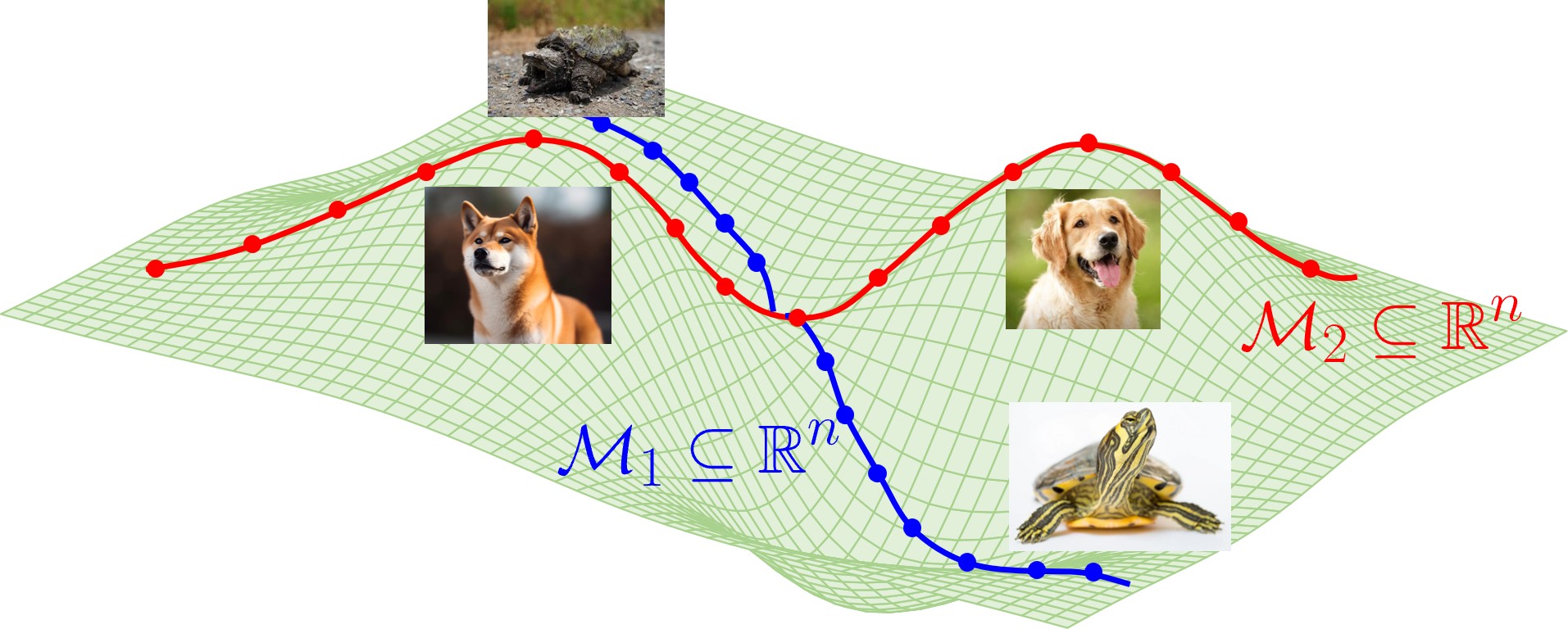
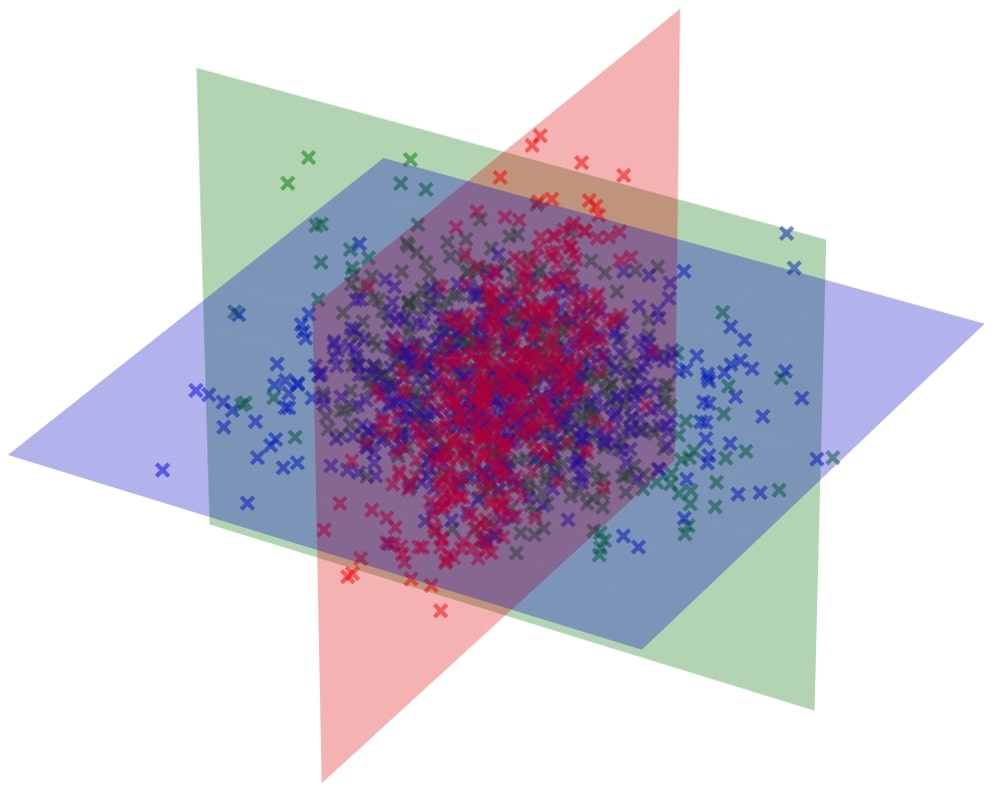
Recent empirical studies have demonstrated that diffusion models can effectively learn the image distribution and generate new samples. Remarkably, these models can achieve this even with a small number of training samples despite a large image dimension, circumventing the curse of dimensionality. In this work, we provide theoretical insights into this phenomenon by leveraging key empirical observations: (i) the low intrinsic dimensionality of image data, (ii) a union of manifold structure of image data, and (iii) the low-rank property of the denoising autoencoder in trained diffusion models. These observations motivate us to assume the underlying data distribution of image data as a mixture of low-rank Gaussians and to parameterize the denoising autoencoder as a low-rank model according to the score function of the assumed distribution. With these setups, we rigorously show that optimizing the training loss of diffusion models is equivalent to solving the canonical subspace clustering problem over the training samples. Based on this equivalence, we further show that the minimal number of samples required to learn the underlying distribution scales linearly with the intrinsic dimensions under the above data and model assumptions. This insight sheds light on why diffusion models can break the curse of dimensionality and exhibit the phase transition from failure to success in learning distributions. Moreover, we empirically establish a correspondence between the subspaces and the semantic representations of image data, facilitating image editing. We validate these results with extensive experimental results on both simulated distributions and image datasets.